A project's real value depends on the project's cash flows and on how those cash flows are statistically related to market variables¹ . It is, therefore, important to understand how to estimate the relevant statistical relations, and we review the basics here because beginning students often do it incorrectly, leading to large errors in valuation. The essential statistical relations are expected values, variances, and covariances of cash flows and market prices. Often correlation (obtained from variances and covariance) is used as well. The variances and covariances can be estimated from historical data, but it must be done properly.

As an example, suppose that a project's revenue will be directly determined by the price of 16 meg DRAM at a future date (or dates). DRAM is not a commodity that can be meaningfully stored (since it quickly becomes obsolete) and accordingly there is no liquid market for it. Therefore, DRAM price is not a pure market variable. On the other hand, it is clear that the price of DRAM (and expectations of its future price) is reflected in some actual market prices, such as the stock price of Micron Technology, Inc., a company that is a major producer of DRAM. In other words, the price of DRAM and the stock price of Micron Technology are probably correlated.

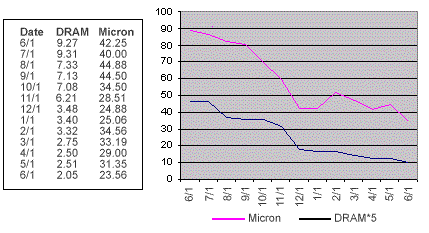
Figure 1. Monthly values of the price of DRAM and Micron Technology stock.

We can verify this conjecture by looking at the data in Figure 1 which shows the prices of 16 meg DRAM (as determined by negotiation between a large buyer and a large seller) and Micron Technology stock from June 1997 to June 1998. Casual inspection of the corresponding graph indicates that there is a tendency for the two to move together.

Correlation can be estimated from this data² . Frequently, students do this by estimating the direct variances and covariances of the data.

Let us see how the typical student calculation would be made. If there are n historical values 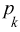of the price of Micron Technology stock price, the direct expected value of these values, is estimated by simply averaging the historical values. In equation form this estimate is

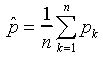
The data represented in Figure 1 consists of 12 monthly values. Using the values for Micron Technology stock price in the averaging formula, we find the estimate of the average stock price to be $33.56. (This value can be found by using the AVERAGE funciton in Excel.) The corresponding variance is estimated by (essentially) averaging the squared differences of the historical values from the expected value. Or, equivalently,

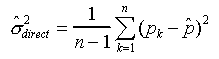
where n -1 is used in the denominator (instead of n ) to account for the fact that the estimate of the expected value, rather than the true expected value, is used on the right hand side. For the data of Figure 1, the variance of the Micron Technology stock price is 55.47 (dollars squared). (This value can be obtained by using the VAR function in Excel.) The standard deviation is defined to be the square root of the variance, which in this case would be estimated to be the square root of 55.476, or $7.44.

Likewise, if there are n corresponding values 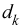of DRAM price, the direct covariance of the Micron Technology stock price and DRAM is estimated as

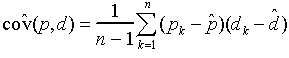
which for the data of Figure 1 is 15.23 (dollars squared). (This value can be obtained by using the COVAR function of Excel and multiplying the result by n/(n-1) = 13/12.)

The correlation between p and d is equal to the covariance divided by the product of the standard deviations, which for the data of Figure 1 works out to be .76 = 76%. This is a pretty high value of correlation and a student might conclude that the price of DRAM is nearly a market variable and accordingly should be heavily discounted in a cash flow valuation.

But this conclusion, and the procedure used to reach it, is not appropriate for deducing correlation for purposes of determining the economic value of the project whose cash flows are determined by DRAM prices. The correct correlation value is quite different than the 76% value.

Correct Method. The procedure discussed above is flawed because the statistical quantities that are relevant for valuation should be based on the period-by-period percentage changes in the prices (or cash flows), not the direct values. More exactly, it is the period-by-period difference in the logarithm of prices or cash flows that should be used. Consider, for example, a stock price that increases exponentially (or geometrically) with no variability - say

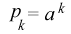
An historical sequence of prices of this stock will have values, most of which will differ from the average value. Hence, such a price sequence will yield a variance estimate that is positive if the above procedure is used. However, the percentage change is

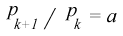
is constant - as is the logarithmic difference

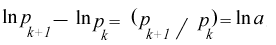
Hence, the variance determined this way is zero as it should be since there is no uncertainty.

For the DRAM example, we should first convert the sequences of DRAM prices and Micron stock prices to sequences of their change in logarithms. Note that these sequences have only 12 elements instead of 13. The resulting sequences are plotted in Figure 2. The correlation between the two sequences is quite apparent.

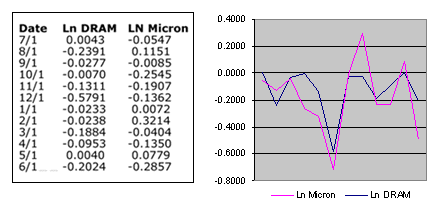
Figure 2. Monthly changes in the logarithms of the prices of DRAM and Micron Technology stock.

We can now apply the estimation formulas to this set of data. This leads to a correlation coefficient (between the log of DRAM price and the log of Micron Technology stock price) of 24% which is much smaller than the 76% figure obtained earlier. This value of 24% is the correct value for the standard method of valuation. Since it is relatively small, we expect that the discount rate that should be applied to DRAM prices is substantially lower than the expected growth rate of Micron Technology stock. Of course, other stock prices are also correlated with the price of DRAM and these should be used as well in a complete analysis.

¹For example, if project cash flows are completely independent of market variables, they are private variables and project value can be found by discounting expected cash flows at the risk-free rate. If cash flows are fixed multiples of a market price, they are market variables and project value is found by discounting expected cash flows at the growth rate of the market price. The complete formulas for valuation will be reviewed in another newsletter.

²Although in practice, weekly data might be used to determine actual estimates, we can illustrate concepts with this small sample.